Rapport.

Introduction

This is a summary of my internship at True AI. During 6 months, I joined their deep learning team based in London and work on state of the art model for dialogue modeling, text understanding and text generation. While this has been an amazing human experience, I’ve also a lot about neural network, software development, and how to build a viable product.

Thanks

I would like to thank the team at True AI for hosting me, in particular Pyry Takala (CEO at TrueAI), and Abhishek Aggarwal (CTO at True AI) for giving me the opportunity to work with them. We had to solve very hard problem together, and I couldn’t have done with them. The core team I’ve been working with has also been extraordinary partner. I’ve learned a lot from you. I couldn’t have found better colleague for an internship. For this reason, I would like to thank deeply Bjorn Mattson, Panagiotis Agis Oikonomou Filandras, and Tim Barnes. I would like to thank the INSA Rouen and all its teachers for having formed me a solid foundation in mathematics and computer science which allows me today to work on any problem with the confidence that I can solve it. INSA Rouen also gave me the opportunity to go abroad and explore the world. I learned a lot at Polytechnique Montréal, and particularly at the research laboratory MILA, where I worked there for a year. Thanks to Professor Knippel for mentoring me during my internship, but also, from a more personal point of view, for giving me a passion for algorithms.

Thanks for my family who supported me from distance during my university time.

True AI

When Artificial intelligence meets customer support! True AI mission is improving customer experience and save precious agent time. They have developed an AI-based software system that learns to reply to conversations, making customer service semi-automatic. True AI team members have decades of research and engineering experience. Our algorithms are built upon cutting edge deep learning breakthroughs.

• True AI has been founded
• True AI are experts in using Artificial Intelligence technology to make customer service agents more productive
• True AI’s product automatically proposes answers to incoming queries based on historic conversations. This means agents can quickly select a recommendation rather than manually type their answer
• True AI can classify cases and route tickets quickly and easily
• True AI can elicit customer data for further processing
• True AI will easily handle repetitive questions, freeing up agent time for more useful tasks
• True AI’s automation tool has been shown to increase agent productivity instantly with even better results emerging over time

Machine Learning

Machine learning is a field that focuses on drawing conclusions from large amounts of data. This is done by letting a model find structures and relationships in the data. By presenting a machine learning model with samples from a data set the model learns to represent hidden relationships and patterns in the data. This process is commonly referred to as training. After training the algorithm is supposed to be able to generalise what it has learned to new, unseen, samples. The ability of machine learning models to generalise to new data points is what engineers and researchers that choose to use machine learning methods are most interested in.

The field of machine learning combines computation and statistics. Computational power is needed in the training procedure, which sometimes can take weeks even on computers built especially for the purpose. Statistics is used to derive the mathematics behind the machine learning models. It can be argued that the main reasons for the increased attention to machine learning during recent years are the increased processing power of modern computers and the large amounts of data easily accessible in today’s digital society.

Supervised Learning

Supervised learning is about finding a predictive model that maps inputs to outputs. To achieve this the learning algorithm is presented with examples of input and output pairs. The goal of the learning process is to produce a function that gives the desired output for inputs that have not been presented to the algorithm during training. It is achieved by fitting internal parameters, often referred to as $\theta$, to the data it tries to approximate. The optimal set of parameters found by the algorithm is often denoted \(\hat{\theta}\). The focus in supervised learning is to find a model that as good as possible maps unseen inputs to outputs. This is clearly similar to well known techniques as e.g. ordinary least squares. We want to use the data to make forecasts about future data points. In machine learning the models are generally very flexible and the internal parameters can thus recreate many different types of patterns in the data. However, the downside of this is that the values of the fitted parameters cannot easily be analysed with statistical rigour, and they typically lack structural or causal interpretation. This in contrast with ordinary least squares, where the fitted parameters, \(\hat{\beta}\), can be used to understand causal relationships in the data.

Supervised learning can further be broken down into classification and regression problems. In classification problems the data points belong to two or more classes, and the problem is to assigns unseen inputs to the correct class. In regression, on the other hand, the outputs are continuous rather than discrete and cannot be summarised into classes.

Machine Learning Model used in this report

Artificial Neural Network

An artificial neural network is a computational model loosely inspired by biological nervous systems. It is basically a network structure built up by a large number of interconnected processing units. Artificial neural network are often simply referred to as neural networks. A good overview of neural networks was presented by LeCun et al. in (2015). Nielsen (2015) has pedagogically described the technique in detail. The neurons or nodes of the network can simply be seen information-processing units. In neural networks these processing units are typically arranged in layers. Signals are passed to the input layers and then they travel through the network to the output layer. Layers between the input and output layers are called hidden layers.

Neural networks can be seen as very complex functions that for a given input $X$ generates an output $Y$. The parameters of the function are called weights. The number of layers defines the depth of the network and the number of nodes in a layer is the width of that layer. In addition to these parameters there are so called weights of each interconnection and activation functions that maps the weighted input signal to an output activation. One of the most important features of a neural network is the non-linearity [^bishop2006pattern]. Neural networks can approximate non-linear relations that typically cannot be reproduced by linear models. The non-linearity is introduced by non-linear activation functions. Given a set of inputs \(x_1, x_2, \ldots, x_N\) a weighted sum of the inputs is formed as $a_j = \sum_{i}^{N} w_{i,j} \cdot x_i + b_j$ where \(w_{i,j}\) are the network weights, $x_i$ the inputs and \(b_j\) the bias term. Here \(a_j\) is the activation, which is the signal that activates the neuron. From the activation the output is computed by applying the activation function to the activation.

Feedforward Neural Network

The feed forward neural network (FFNN) is the most simple type. The network has only forward pointing connections and the nodes are structured in layers. In the next figure, a schematic drawing of interconnected nodes in a FFNN is shown.

Activation functions

The activation function is what makes neural networks to non-linear classifiers. Until recently the sigmoid function $\sigma (x) = \frac{1}{1+e^{-x}}$

and the hyperbolic tangent function

$$f(x) = \tanh(x) = \frac{2}{1+e^{-2x}}-1$$

have been the most commonly used activation functions. The most important difference between these two functions is the output range. As can bee seen in the next figure, the sigmoid function returns a value in the range [0,1] and the hyperbolic tangent function a value in the range [-1,1]. Lately, another activation function called the rectifier is mostly used. The rectifier is in the context of neural networks defined by $g(z) = \max \{0,z\}$ and has range [0,\(\infty\)] [^hahnloser2000digital]. A unit in a neural network implementing the rectifier is called a rectified linear unit (ReLU) and for this reason the activation type often is referred to as simply ReLu. In the next figure, the three mentioned activation functions are drawn in the interval [-5,5].

The major advantage of the rectifier compared to both the sigmoid and hyperbolic tangent functions is that it overcomes the problem of vanishing gradients. The gradients of these functions quickly vanishes as $x$ grows. The gradient of the rectifier does not do this: $\frac{\mathrm{d} }{\mathrm{d} x} g(x) = \left\{\begin{matrix} 0 & x < 0\\ 1 & x > 0 \end{matrix}\right.$

Stocastic Gradient Descent

Gradient descent is an optimisation algorithm where an optimum is found by incrementally taking steps in the direction of the negative gradient of the cost function. One gradient descent step is described by: $\mathbf{w}^{(\tau + 1)} = \mathbf{w}^{(\tau)} - \eta \nabla_{\mathbf{w}} E(\mathbf{w}^{(\tau)}, \mathbf{d}),$ where \(\eta\) denotes the step length (sometimes referred to as learning rate), \(E\) the cost function, \(\mathbf{w}\) i this case the set of weights and \(\mathbf{d}\) the data used to calculate the cost and \(\tau\) defines the current time-step. In the gradient descent algorithm the cost function is computed for the complete training set. Hence, the weights will only be updated once for every one pass over the complete training set. When working with very large data set such a method becomes very slow and inefficient. Stochastic gradient descent is a method that seeks to solve this problem. It is a stochastic approximation of the gradient descent method that is used to reduce the required number of mathematical operations to optimise the model. The method reduces the computational cost of each update by approximating the gradient from a stochastic sample subset. This way the weights are updated more frequently. Instead of one update per epoch there is one update per batch (a subset of examples taken from the data set). This efficiency is fundamental in large-scale machine learning problems. The algorithm can be summarised as:

Seq2Seq Models for Short Answer Generation

Recurrent Neural Networks (RNN) are a particular kind of artificial neural networks that are specialized in extracting information from sequences. Unlike simple feedforward neural networks, a neuron’s activation is also dependent from its previous activations. It allows the model to capture correlations between the different inputs in the sequence.

However, this type of architecture can be very challenging to train, partly because it is much more prone to exploding and vanishing gradients ¹. These problems can be overcome by choosing more stable activation functions like ReLU or tanh and by using more sophisticated cells like LSTM and GRU, which involve more parameters and computations than the vanilla RNN cell but are designed to avoid vanishing gradients and capture long range dependencies ².

In the recent years, RNNs along with the mentioned strategies have been able to achieve state of the art level of performance on many challenging tasks like conversational models ³, machine translation ⁴ and automatic summarization ⁵. In this project, we implement a sequence to sequence (Seq2Seq) model using two independent RNNs, an encoder, and a decoder. We use the Cornell Movie dialog data set to train a short text answering model similar to the work of Shang et al. ⁶. We also explore the use of similar models on custom data sets of Facebook-Messenger conversation histories.

A bit of theory

Recurrent Neural Networks

In a regular RNN, at time-step \(t\), the cell state \(h_t\) is computed based on its own input and the cell state \(h_t\) that encapsulates some information from the precedent inputs :

$$h_t = f(W^{hx}x_t + W^{hh}h_{t-1})$$

In this case \(f\) is the activation function. The cell output for this time-step is then computed using a third series of parameters \(W^{hy}\) :

$$y_t = W^{hy}h_t$$

With LSTM or GRU cells, the core principle is the same, but these type of cells additionally use so-called gates that allow to forget information or expose only particular part of the cell state to the next step.

Sequence to Sequence

Sequence-to-sequence models (or RNN encoder-decoder) have first been introduced in 2014 almost simultaneously by two different research groups ⁷, ⁸. They have recently emerged as the new way-to-go for various generative tasks. The principle of Seq2Seq architecture is to encode information on an input sequence \(x_1\) to \(x_T\) and to use this condensed representation known as context vector to generate a new sequence \(y_1\) to \(y_{T^{‘}}\). Each output \(y_t\) is based on previous outputs and the context vector :

$$p(A|Q) = p(y_1, y_2, ..., y_{T^{'}}|x_1, x_2, ..., x_T) = \prod_{t=1}^{T^{'}}p(y_{t}|c_t, y_1, ..., y_{t-1})$$

The loss \(\ell\) is the negative log-probability of the answer sequence \(A = [y_1, …, y_{T^{‘}}]\) given the question sequence \(Q = [x_1, …, x_T]\), averaged over the number \(N\) of \((Q,A)\) pairs in a minibatch :

$$\ell = -\frac{1}{|N|}\sum_{(Q,A)\in N} p(A|Q)$$

Multiple layers of RNN cells can be stacked over each other to increase the model capacity like in a regular feedforward neural network.

The following figure presents a Seq2Seq model with a two layers encoder and a two layers decoder:

It is also common to have different weights for encoder and decoder cell:

$$W^{h*}_{encoder} \neq W^{h*}_{decoder}$$

Attention Mechanism

Theoretically, a large enough and well-trained model should be able to perform well on predicting the best decoding sequence given the encoding ones. Indeed, neural networks are universal function approximators ⁹ , which means they theoretically can model any function, even the conditional distribution \(p(y_1, y_2, …, y_T|x_1, x_2, …, x_T)\). However, in practice, we don’t have unlimited data, so we need to have a proper inductive bias, that will allow the network to learn to model accurately with a reasonable amount of data.

The first bottleneck with the previous model is that all the relevant information to decode is fed through a fixed size vector. When the encoding sequence is long, it often fails to capture the complex semantic relations between words entirely. On the other hand, if the fixed size vector is too large for the encoding sequence, this may cause overfitting problem forcing the encoder to learn some noise.

Furthermore, words occurring at the beginning of the encoding sentence may contain information for predicting the first decoding outputs. It is often complex for the model to capture long term dependencies, and there is no guarantee that it will learn to handle these correctly. This problem can be partially solved by using a Bi-Directional RNN (BD-RNN) as the encoder. A BD-RNN will encode its input twice by passing over the input in both directions:

It allows for hidden representations at each timestep to capture both future and past context information from the input sequence.

However, to better overcome the information bottleneck and long-term dependencies limitations, attentions model have been introduced. The basic idea of attention is that instead of attempting to learn a single vector representation for each sentence, we keep around vectors for every word in the input sentence, and reference these vectors at each decoding step.

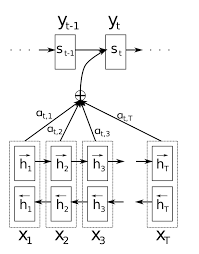
• Outputs from the encoder cell are usually used as attention vectors. We will call them \(h_{j}\text{, } \forall j \in [1, T]\). From the original paper ¹⁰ equation, a 1-layer MLP is used to learn a combination of the decoder previous hidden vector \(s_{t-1}\) and all the attention vector output \(h_{j=1,…,T}\).

  $$b_{tj} = v_{a}^{T}tanh(W_{a}s_{t-1} + U_{a}h_{j})$$

  The optimization algorithm should learn to produce large \(b_{tj}\) when the \(j\)th attention vector is relevant for decoding the \(t\)th token.

• The \(1D\) vector \(b_{t} = (b_{t0}, … ,b_{tT})^T\) is then passed through a softmax function. One reason to compute the softmax is to keep the math as correct as possible. Removing the softmax may cause values in $b_{t}$ to increase continuously with training while competing against each other to be the most relevant vector to use. Hence, we can see the softmax function as a regularizer. $\alpha_{tj} = softmax(b_{tj}) = \frac{exp(b_{tj})}{\sum_{k=1}^{T} exp(b_{tk})}$

• The final context vector is computed as a convex sum of every attention vector:

  $$c_t = \sum_{j=1}^{T}\alpha_{tj}h_{j}$$

  This vector is finally concatenated with the decoder input. The following figure summarizes how the attention mechanism works:

Seq2Seq tricks

Beam Search

Beam search is a well-known heuristic search algorithm, which has been widely adopted in large systems with an insufficient amount of memory to store the entire search tree. In the context of sequence generation, and when a model is already trained, the decoder predicts the next token as the

$$\arg\!\max_{k \in |K|}(softmax(y_{tk}))$$

where \(|K|\) is the decoder vocabulary size. Because the model has been trained with maximum likelihood, the most probable answer is not always the best, and maybe the second best choice of word will condition a better answer. Keeping the \(M-\)best word prediction at every time step is what beam search does.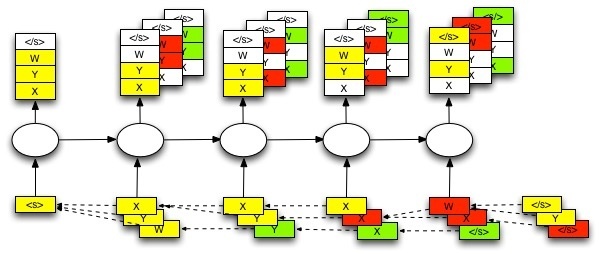

Sample softmax

During training, the predicting token \(y_k\) is computed with the softmax function, and as |K| is usually larger than the RNN cell hidden size |h|, a dictionnary matrix \(W \in \mathbb{R}^{|K|, |h|}\) is constructed. Every row \(w_k\) becomes the learned representation of a token \(y_k\).

In essence, the softmax forces the learning algorithm to orientate row vector \(k\) of \(W\) in the same direction of the output of the cell when \(k\) should be the predicted token, so that the future softmax function will return a larger value at index \(k\).

However, as \(|K|\) becomes large, computation is a bottleneck. A strategy, introduced by ¹¹, proposes to alleviate this problem by selecting a small subset of target vocabulary.

Remember that for :

$$p(y_t = y_k|y_{lt; t}, x) = e^{w_k^Tg(y_{t-1}, h_t, c_t)} / \displaystyle{\sum_{k^{'} \in K} e^{w_{k^{'}}^Tf(y_{t-1}, h_t, c_t)}}$$

The main idea of the proposed approach is to approximate the second term of the gradient (i.e ^{i.e 1} , by importance sampling ^{i.e 2} using a smaller number of target words. ^{i.e 3}

The subset \(K_i\), which contains target words, are computed before training:

• Every training decoding sequence \( A_j = (y_1, y_2, …,y_{T^{'}}) \) is assigned to a cluster \(K_i\). Hence \( (y_{1:T^{'}})_j \in K_i\).

• Until \(|K_i| \lt S\) (\(S\) is an hyperparameter), new training sentences are appended to the cluster.

Conclusion: Sample softmax is a simple method to compute an approximation of the full softmax when the decoder vocabulary size \(K\) is large. Instead of moving the correct target word vector \(w_k\) in the direction of the \(y_t\), while pushing all others word vector away, it only moves a subset of them. It is why we used sample softmax in every model involving word level decoding.

Non-Maximum Likelihood approach

Maximum Likelihood suffers from predicting the most probable answer. It lacks some belief concerning the appearance of a token in the vocabulary, hence a model trained with maximum likelihood will tend to output short general answers that are very common in the vocabulary, like yes, no, maybe. It is a huge problem for conversation diversity. Different approaches have been proposed as a remedy for this issue.

Mutual Information Loss

One approach was to use Maximum Mutual Information ¹²

$$\displaystyle{\hat{A} = \arg\!\max_Q\text{ }log\frac{p(A,Q)}{p(A)p(Q)}},$$

which measure the mutual dependence between inputs (i.e., Q) and the output (i.e., A), instead of Maximum Likelihood

$$\displaystyle{\hat{A} = \arg\!\max_Q\text{ }log(p(A|Q))}$$

From this, we can derive a nicer form for the maximization problem

$$\arg\!\max\text{ }log(p(A|Q) - \lambda log(p(A))).$$

As we want to control how we should penalize generic answers, a \(\lambda\) is added before the second term. Price-Bayes theorem also tells us that

$$\displaystyle{\hat{A} = \arg\!\max_Q\text{ } (1 - \lambda)log p(A|Q) + \lambda log p(Q|A)}.$$

This is still unsatisfiable because both penalizer term are nontrivial to use:

1. \(p(A)\) penalizer leads to ungrammatical responses. To overcome this issue, \(p(A) = \prod_{t=1}^{T^{'}} p(y_t|c_t, y_1, y_2, …, y_{t-1})\) is approximated by multiplying probability at every timestep with an explonential decay \(g(t)\). The reason for this is that first words to be predicted are determinant for the remainder of the sentence. Hence penalizing words early in the sentence encourage diversity in the predicted output sequence.

2. \(p(Q|A)\) is intractable while decoding. One strategy employ in Li et al. ¹³ was to employ a second seq2seq model which predict \(p(Q|A)\). First, a classic seq2seq predicts the conditional probability \(p(A|Q)\) using beam search. Then all \(M\) prediction are passed as input to the inverse seq2seq, and the loss function is added as a penalized term.

Adversarial Loss

Another elegant way to force more diverse and grammatically correct answers would be to use Generative Adversarial Networks (GANs) ¹⁴. In this case, having a discriminator conditioned as well on the question sequence \(Q\) and classifying output sequences as being real or fake should be able to detect common generic answers that the generator tends to produce. The vanilla GAN objectives can be thought of as a minimax game played between the Generator (\(G\)) and the Discriminator (\(D\)) with the dueling objectives : \(\min_{G}\max_{D} V(D,G)\), where:

\(V(D,G) = E_{x \sim p_{data}(x)}[\log D(x)] + E_{z \sim p_{z}(z)}[\log(1-D(G(z)))]\)

In this case, \(x\) is a sample of the real data distribution (\(p_{data}\)), and \(z\) is usually noise drawn from a known distribution (\(p_z\)) easy to sample from (Gaussian or uniform). When training is succesfull, \(G\) will have learned to map any noise sample \(z\) to “real-looking” samples \(G(z)\).

In our case, however, our generator could be the decoder from our seq2seq model, and would, therefore, learn to map sentence encodings to real data samples. This would yield that \(z\) from the GAN formulation would be replaced by \(Enc_G(Q)\) where \(Enc_G\) is the encoding function of the seq2seq. Our discriminator, to judge answers according to the questions and not just as real-looking samples, should also be conditioned on \(Q\). In this case, a possible strategy would be to provide the discriminator another sentence encoder \(Enc_D\) to provide a fixed sentence representation to an RNN performing per time-steps predictions on either real answers our fake ones produced by \(G\). This way, the discriminator RNN could output predictions, on each time step, concerning (1) its previous state and (2) the global representation of \(Q\), producing direct learning signals for the generator at every time step. Our minimax game value would then look like this :

$$V(D,G) = E_{Q \sim p_{data}(Q)}[\log D(A|Q)]$$ $$+ E_{Q \sim p_{data}(Q)}[\log(1-D(G(Enc_G(Q))))]$$

Discrete outputs and REINFORCE Algorithm

Although using GANs for dialogue generation is appealing, one major obstacle would prevent us from applying the idea presented above: the fact that output sequences from the generator, as well as exact answer sequences are sequences of discrete tokens. Therefore, gradients from the discriminator prediction errors, could not get propagated back passed the \(argmax\) operation over the outputted probability distribution of symbols in the generator at each time step.

Luckily, methods from the field reinforcement learning offer ways to learn from reward signals despite the choice of discrete actions. Specifically, if we consider the \(softmax\) output of \(G\) as being a policy \(\pi\) for discrete actions (word or char tokens) given the state (\(S_t\), given by the hidden state of the decoder), on could frame this problem as a reinforcement learning one, en employ a policy-gradient technique, such as the REINFORCE algorithm ¹⁵. This approach has been applied successfully to text generation ¹⁶. In our case, however, using an RNN discriminator, outputting rewards at each time step could potentially remove the need for Monte-Carlo search, as we could trivially compute real, complete returns as sums of reward from each \(t \in T^{‘}\). Moreover, adding conditioning on the question representation would allow for answer generation instead of primary text generation.

Experiments and results

Network Architectures

We performed experiments with multiple variants of the sequence-to-sequence architecture described above. As sequence to sequence model offers loosely coupled encoder and decoder networks, one can quickly change input or output data formats without changing the structure. Of course, re-training is then needed. In our case, we experimented with different language abstraction levels for both the encoder and decoder. We compared word-level and character-level representations of sentences as input or output formats. We experimented with three variants: word2word, word2char, and char2char, where for example word2char represents a word-level encoder coupled with a char-level decoder.

In all cases, for encoder and decoder networks, we used three stacked GRU hidden layers of each 256 cells. Feed-forward dropout, when applied, was used with a probability of 0.25 of dropping units, and the Adam optimizer was used to minimize the negative log-likelihood.

Data

We focused our empirical study on a movie-dialogue dataset while also experimenting on some custom dataset of Facebook Messenger conversations, retrieved from the author’s history of discussions.

Cornell Movie Dialog Corpus

This dataset contains movie conversations extracted from scripts of 617 movies, between more than 10 000 characters. We extract first Q/A pairs of each conversation and retrieve more than 120 000 samples. We apply two preprocessing strategies to extract the 8000 most common words or our arbitrary vocabulary of 55 characters. Most sentences contain common, well-written words and we, therefore, consider this as our clean dataset.

Messenger Conversations

As it is possible for one to retrieve his/her own Facebook conversations’ history, the authors wanted to experiment with this data and find out if a trained seq2seq on this data could reflect one’s style of written dialogue. However, some serious limitations of the data made it hard for a network to output answers strongly linked semantically to the input query. First, the data is limited, and unbalanced given different authors, as shown in the Table below : Secondly, as humans often do on Facebook, the authors do not always have a clean or proper spelling when on Facebook, compared to when writing more official documents, or compared with the movie dialogue corpus. Moreover, a network trained on the clean movie data, could not be used as a pre-trained model for Messenger as this dataset contains only English sentences, while authors are all French speakers. For these reasons, experiments done with these datasets were all done on a character-level encoder and decoders.

Results

Cornell Movie Dialog Corpus

Char2Char, no attention, no dropout

Without Droupout, learning curves produced while training looks like this for most models: 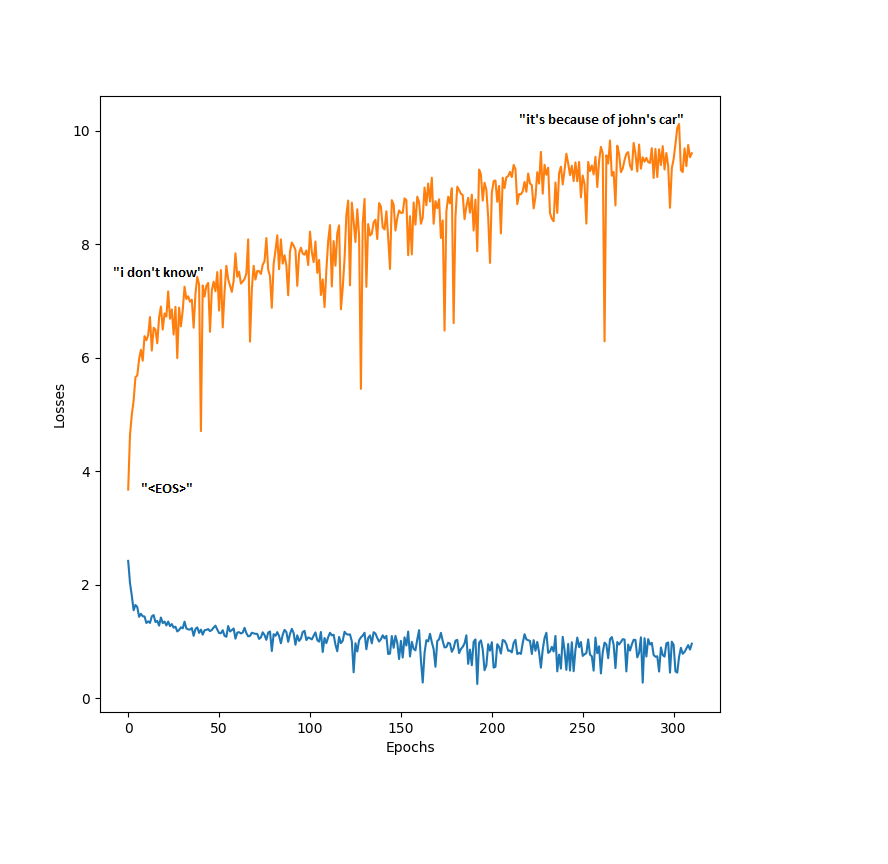curves for the word2word architecture. Each epoch consisted of 250 iterations in which a random mini batch is fed to the network. The labels present on the Figure are standard outputs of the network at different training phases. One common behavior in our experiments was the way networks started of being very boring on the validation set and evolved to being somewhat entertaining on the validation set, despite having a larger loss. This is directly linked to the negative log-likelihood loss function. Therefore, overfitting in the case where we aim at entertaining dialogues with little training data might not be a bad thing. Learning some answers, that are grammatically correct from the training set has at least the advantage of creating less ambiguous answers than “I don’t know” or “Yes”.

Adding attention and dropout

To improve the quality of generated answers, we added the attention mechanism described above, so that it can be easier for the network to use specific words from the question query as conditioning information. Also, we added feed-froward dropout to help generalization of the model. We list here training curves and sample answers for fixed, custom questions for different models, and discuss these results in the Discussion section. When using word-level decoders, we used the sample softmax as described above.

Word2Word

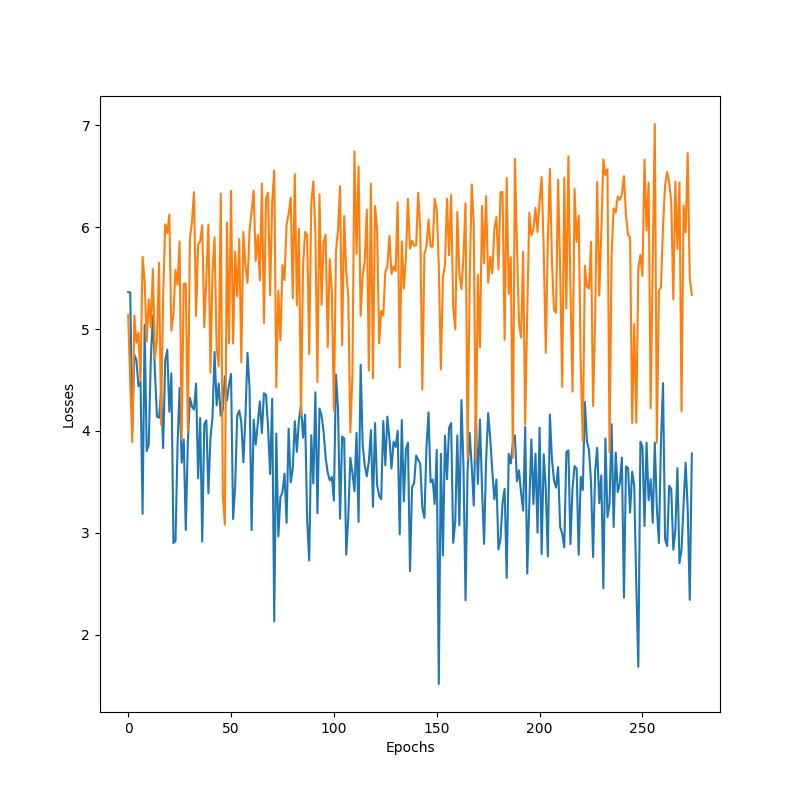
Char2Char

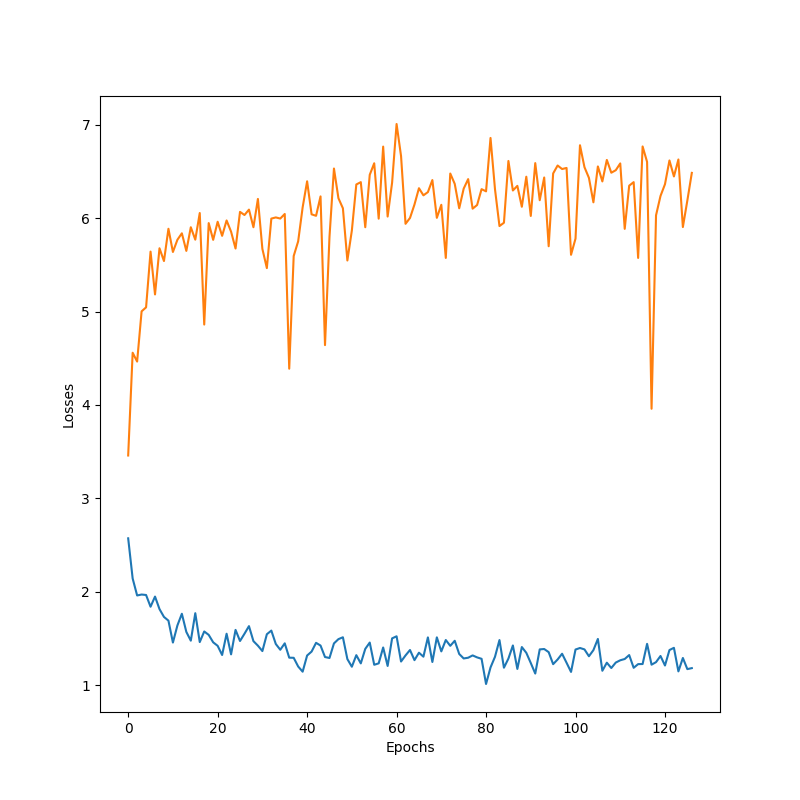
Word2Char

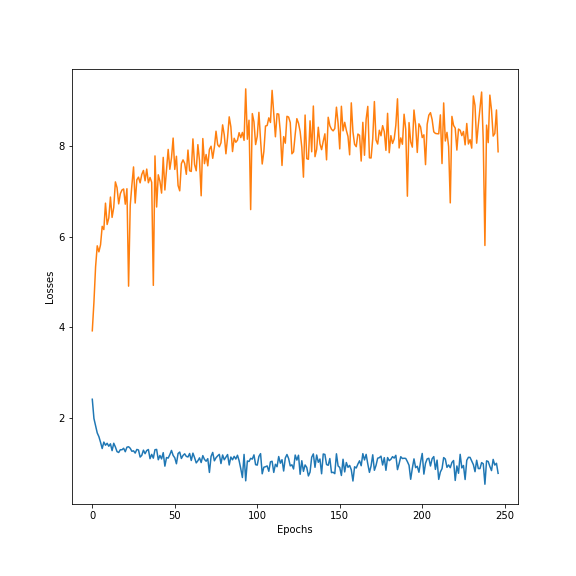
In general, word-level decoders performed worst for answer generations, and char-level decoders learned surprisingly fast to write complete words, as well as punctuation, yielding more realistic sentences. As the curves show, adding attention and dropout seems to help the overall validation performance. However, given the limited data, dropout didn’t allow removing the overfitting occurring almost as soon as training starts.

Capturing style with Messenger

Experiments on the different Messenger datasets were performed mostly out of curiosity and for fun. The main goal here was to assess if a model trained on conversations from one of the authors could capture a bit of his familiar writing style. Indeed, when comparing networks, especially one trained on a French author’s conversation with one trained on a Quebec’s author’s conversations, we could easily assess which network was which. We show some samples below. As explained above, all Messenger bots were trained with char2char architectures.

Even with this insufficient number of samples, the third author, whose conversations were not used, could identify which network was trained on whose conversations, showing some level of style captured by the networks. More precisely, key words like “chill” were not present in the French Messenger corpus, and interestingly, word orderings would sometimes not appear in one of the versions, like the word “quoi” following a whole sentence is not common at all in the Quebec corpus. Even though answers were not often of high quality, it shows that the networks learned common language patterns and writing styles.

Conclusion

We implemented a Seq2Seq model for short text generation. The model has been trained of two different datasets, the Cornell Movie Questions and Answers and the author’s Facebook Chat histories. For the Cornell dataset, three variations of the model have been compared : char2char, word2word and word2char. The three models were qualitatively comparable but word2char might provide slightly more sophisticated answers. For the Facebook dataset, only char2char have been implemented due to the unguaranteed grammatical correctness of the data. The model have proven able to capture each author’s style, with especially visible variations between the French and Quebecer styles. Finally, with more time, we would have liked to improve the attention mechanism results and to implement the GAN approach that uses a discriminator to make our generator reply more naturally.

Footnotes

Footnotes 1: For simplicity, let’s define \(\chi(y_k) = w_k^Tf(y_{t-1}, z_t, c_t) + b_k\). Computing the gradient of \(log(p(y_t = y_k|y_{< t}, x))\) gives us \( \nabla(\chi(y_k)) - E_p(\nabla(\chi(y)))\) where the first term is A sparse vector with \(1\) non zero entry at row \(k\), and the second is a complicated sum \(\displaystyle{\sum_{k^{‘}}\frac{\chi(y_{k^{‘}})}{\sum_{k^{‘’}}\chi(y_{k^{‘’}})}\nabla(\chi(y_{k^{‘}}))}\).

Footnotes 2: In a nutshell, importance sampling is a technique to approximate any distribution properties, by sampling from another, usually simpler, distribution.

Footnotes 3: In their paper ¹¹ approximate the expectation with importance sampling by defining a set of distributions \(Q_i\) with their respective subset \(K_i\):

$E_p(\nabla(\chi(y))) = \displaystyle{\sum_{k^{'} \in K^{'}, \|K^{'}\| lt \|K\|}\frac{Q(y_{k^{'}})\chi(y_{k^{'}})}{\sum_{k^{''}}Q(y_{k^{''}})\chi(y_{k^{''}})}\nabla(\chi(y_{k^{'}}))}$ .

Codes

/TODO add

Bibliography

Sébastien Jean and Kyunghyun Cho and Roland Memisevic and Yoshua Bengio