Predicting House Sales using statistical learning technique and deep learning.
Data introduction
Recently, I’ve spent some time learning about R, and I decide to use my rec House Sales In King County. The dataset is available on this page.
The goal of this project will be to predict the price of a house according to characteristics, such as surface area, number of floors, number of rooms
# Import the data
data <- read.csv("kc_house_data.csv")
Let’s have a look at the insight of the data:
head(data)
## id date price bedrooms bathrooms sqft_living
## 1 7129300520 20141013T000000 221900 3 1.00 1180
## 2 6414100192 20141209T000000 538000 3 2.25 2570
## 3 5631500400 20150225T000000 180000 2 1.00 770
## 4 2487200875 20141209T000000 604000 4 3.00 1960
## 5 1954400510 20150218T000000 510000 3 2.00 1680
## 6 7237550310 20140512T000000 1225000 4 4.50 5420
## sqft_lot floors waterfront view condition grade sqft_above sqft_basement
## 1 5650 1 0 0 3 7 1180 0
## 2 7242 2 0 0 3 7 2170 400
## 3 10000 1 0 0 3 6 770 0
## 4 5000 1 0 0 5 7 1050 910
## 5 8080 1 0 0 3 8 1680 0
## 6 101930 1 0 0 3 11 3890 1530
## yr_built yr_renovated zipcode lat long sqft_living15 sqft_lot15
## 1 1955 0 98178 47.5112 -122.257 1340 5650
## 2 1951 1991 98125 47.7210 -122.319 1690 7639
## 3 1933 0 98028 47.7379 -122.233 2720 8062
## 4 1965 0 98136 47.5208 -122.393 1360 5000
## 5 1987 0 98074 47.6168 -122.045 1800 7503
## 6 2001 0 98053 47.6561 -122.005 4760 101930
# Number of examples
nrow(data)
## [1] 21613
# Number of features
ncol(data)
## [1] 21
This database is made up of a substantial number of examples, which makes it possible to train several models of prediction, and to separate our data into a training set and a validation set.
Data preprocessing
Selecting attributes
Some data are not compelling at all to predict the price, then removing them is legitimate; I am talking about the id, the date, the zipcode, lattitude, and longitude. It seemed to me that it leads to potential confusion for training our models.
data = data[,-c(1:2, 17:19)]
Removing outlier
Removing outliers improve the quality and generalization of trained models. For example, it reduces the variance. As there are many examples, removing some of them is possible. Hence, we’ll remove all outlier of surfaces and price attributes. Also, the explanatory variable * prices * will be deleted. In fact, in Our database is indeed found costly houses, which are usually outlier with a price very different from the rest. Hence they won’t fit any linear model. On the opposite, meager price, is hard to predict for any model. If the model is sufficiently flexible, it may be possible to predict the price of these examples, but this is not what we want. We want a good generalization, not an overfitted model.
remove_outliers <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs=c(.25, .75), na.rm = na.rm, ...)
H <- 4 * IQR(x, na.rm = na.rm)
y =
y = c(which(x < (qnt[1] - H)),which(x > (qnt[2] + H)))
y
}
num = 0
for(name in names(data)){
if(grepl("sqft", name) || name == "price"){
outliers = remove_outliers(data[,name])
num = num + length(outliers)
data = data[-outliers,]
}
}
# Number of data removed
print(num)
## [1] 2030
# Number of daa still available
print(nrow(data))
## [1] 19583
Removing abortive data will, of course, reduce the RSS, MSE calculated from our data. But this will undoubtedly help models converge towards a solution that will generalize better.
Decoralleted features
In order to avoid having too correlated features, it is necessary to remove one of the two variables of the attributes pairs that have an higher correlation than 0.75. Sub-model selection methods had a drop in performance when the explanatory variables are too correlated.
tmp = cor(data)
tmp[lower.tri(tmp)] = 0
diag(tmp) = 0
data1 = data[, !apply(tmp, 2, function(x) any(x > 0.75))]
setdiff(names(data), names(data1))
## [1] "sqft_above" "sqft_living15" "sqft_lot15"
Three variables were removed from the model. These are sqft_above, sqftliving15, sqft_lot15. They are indeed very correlated with the variable sqft_living.
Transforming numerical data
All data is numeric. Variables such as bathrooms, bedrooms, floors will be left as a numeric variable, because the difference between these values is interpreted relatively well, and it won’t harm any model. However, it’s not the case of variables like condition, view and grade. Condition has three maximum factors, while grade has at least five. So it is better to convert them as dummy variables. A function is created for it.
as.dummy_variable = function (data){
data$floor = factor(data$floor)
data$view = factor(data$view)
data$condition = factor(data$condition)
data$grade = factor(data$grade)
return(data)
}
Splitting between training and testing time
The data will be separated into two groups, the training of our models. For this, the * sample * method will be used:
smp_size = floor(0.7 * nrow(data))
train_ind = sample(seq_len(nrow(data)), size = smp_size)
train = data[train_ind,]
test = data[-train_ind,]
Some statistics
The function summary will be used and get some statistics on our explanatory variables (mean, minimal, maximal, variance, median)
summary(data)
## price bedrooms bathrooms sqft_living
## Min. : 78000 Min. : 0.000 Min. :0.000 Min. : 290
## 1st Qu.: 315000 1st Qu.: 3.000 1st Qu.:1.500 1st Qu.:1400
## Median : 439000 Median : 3.000 Median :2.250 Median :1850
## Mean : 506314 Mean : 3.348 Mean :2.071 Mean :1988
## 3rd Qu.: 620000 3rd Qu.: 4.000 3rd Qu.:2.500 3rd Qu.:2440
## Max. :1928000 Max. :33.000 Max. :7.500 Max. :6630
## sqft_lot floors waterfront view
## Min. : 520 Min. :1.000 Min. :0.000000 Min. :0.0000
## 1st Qu.: 4976 1st Qu.:1.000 1st Qu.:0.000000 1st Qu.:0.0000
## Median : 7245 Median :1.000 Median :0.000000 Median :0.0000
## Mean : 7824 Mean :1.487 Mean :0.004136 Mean :0.2046
## 3rd Qu.: 9604 3rd Qu.:2.000 3rd Qu.:0.000000 3rd Qu.:0.0000
## Max. :32481 Max. :3.500 Max. :1.000000 Max. :4.0000
## condition grade sqft_basement yr_built
## Min. :1.000 Min. : 1.000 Min. : 0.0 Min. :1900
## 1st Qu.:3.000 1st Qu.: 7.000 1st Qu.: 0.0 1st Qu.:1950
## Median :3.000 Median : 7.000 Median : 0.0 Median :1972
## Mean :3.411 Mean : 7.565 Mean : 282.7 Mean :1970
## 3rd Qu.:4.000 3rd Qu.: 8.000 3rd Qu.: 550.0 3rd Qu.:1997
## Max. :5.000 Max. :12.000 Max. :2610.0 Max. :2015
## yr_renovated
## Min. : 0.00
## 1st Qu.: 0.00
## Median : 0.00
## Mean : 79.92
## 3rd Qu.: 0.00
## Max. :2015.00
Simple regression with a single explanatory variable
The explanatory value used will be the most numerical correlated with the price variable:
cor_matrix = cor(data)
cor_matrix[,"price"]
## price bedrooms bathrooms sqft_living sqft_lot
## 1.00000000 0.30598400 0.48186574 0.66031611 0.11239660
## floors waterfront view condition grade
## 0.26696595 0.14587787 0.36062051 0.05249493 0.66324669
## sqft_basement yr_built yr_renovated
## 0.30394940 0.02994293 0.13446924
The most correlated numerical explanatory variable is sqft-living.
Price as a function of the living surface
lm.fit =lm(price ~ sqft_living, data=train)
summary(lm.fit)
##
## Call:
## lm(formula = price ~ sqft_living, data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -752305 -138675 -21914 101686 1243428
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 53371.070 4714.600 11.32 <2e-16 ***
## sqft_living 227.143 2.197 103.37 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 206900 on 13706 degrees of freedom
## Multiple R-squared: 0.4381, Adjusted R-squared: 0.438
## F-statistic: 1.069e+04 on 1 and 13706 DF, p-value: < 2.2e-16
lm.pred = predict(lm.fit, test)
lm.rmse = sqrt(mean((lm.pred - test$price) ^2) )
# Racine carée du MSE du modéle
lm.rmse
## [1] 209455.5
According to the adjusted \(R^2\), the variance in the house price is hardly explained by the data sqft-living. However, the RMSE is high, indicating that the simple linear model is probably incomplete, or too simple. Here is the scatter plot.
pairs(data[, c(1,4)])
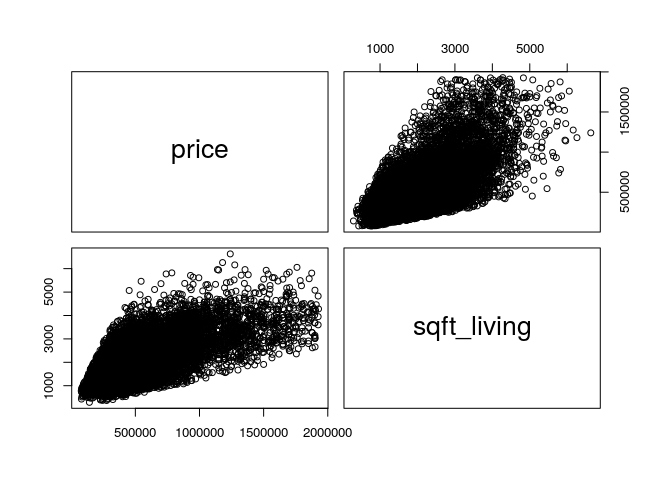
Looking at the curve, it appears that price variability increases with the common area. It is possible to transform linearly the variable sqftliving to see if this improves the quality of the regression.
lm.fit =lm(price ~ I(sqft_living ^ (2)), data=train)
summary(lm.fit)
##
## Call:
## lm(formula = price ~ I(sqft_living^(2)), data = train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1100069 -137821 -26246 98835 1280545
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.906e+05 2.708e+03 107.3 <2e-16 ***
## I(sqft_living^(2)) 4.663e-02 4.470e-04 104.3 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 206100 on 13706 degrees of freedom
## Multiple R-squared: 0.4425, Adjusted R-squared: 0.4424
## F-statistic: 1.088e+04 on 1 and 13706 DF, p-value: < 2.2e-16
lm.pred = predict(lm.fit, test)
sqrt(mean((lm.pred - test$price) ^2) )
## [1] 208662.5
After testing several nonlinear modifications to sqft_living (sqrt, log, \(^2\), \(^3\)), none seems to improve the regression.
LASSO regression
The advantage of the LASSO regression is that it allows selecting among the explanatory variables those that best explain the dependent variable. If the LASSO coefficient β of any explanatory variable tends to zero, then the variable can not influence the prediction of the dependent variable. Depending on the results of the algorithm, some explanatory variables will be removed from the model.
# Transformer les données non numériques en dummy variable
data = as.dummy_variable(data)
train = data[train_ind,]
test = data[-train_ind,]
# LASSO REGRESSION MODEL
x = model.matrix(price ~., data=train)
y = train[,1]
fit.lasso = glmnet(x, y, alpha = 1)
plot(fit.lasso, xvar="lambda", label=T)
legend("bottomleft", names(train[-1]), lty=1, cex=.75)
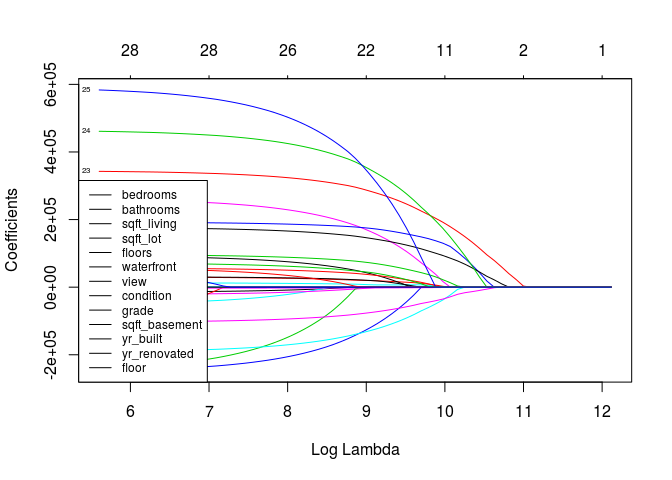
# Optima value of LAMBDA
cv.lasso = cv.glmnet(x,y, alpha=1)
plot(cv.lasso)
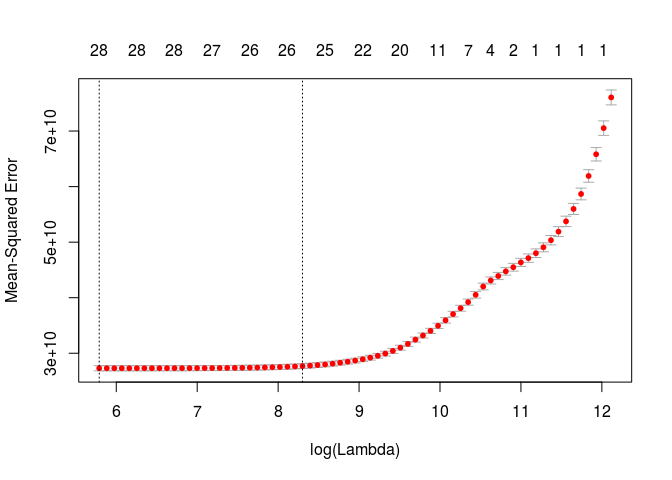
lambda.min = cv.lasso$lambda.min
print(lambda.min)
## [1] 326.739
fit.lasso = glmnet(x, y,alpha = 1, lambda = lambda.min)
fit.pred = predict(fit.lasso, model.matrix(price~.,data=test))
print(paste("RMSE : ", sqrt(mean((fit.pred - test$price) ^ 2))))
## [1] "RMSE : 164778.582907721"
# Coefficient des variables explicatives
coef.lasso = coef(cv.lasso)
coef.lasso
## 34 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 5.357123e+06
## (Intercept) .
## bedrooms -6.316303e+03
## bathrooms 2.477882e+04
## sqft_living 1.223387e+02
## sqft_lot -3.432196e+00
## floors 1.047572e+04
## waterfront 2.170895e+05
## view1 6.868382e+04
## view2 4.775761e+04
## view3 8.550401e+04
## view4 1.843535e+05
## condition2 -1.091966e+04
## condition3 -1.250071e+04
## condition4 .
## condition5 2.613684e+04
## grade3 .
## grade4 -1.125385e+05
## grade5 -1.898672e+05
## grade6 -1.627385e+05
## grade7 -9.070637e+04
## grade8 .
## grade9 1.621404e+05
## grade10 3.167587e+05
## grade11 4.110048e+05
## grade12 4.716455e+05
## sqft_basement 7.570816e+00
## yr_built -2.588052e+03
## yr_renovated 1.174276e+01
## floor1.5 .
## floor2 .
## floor2.5 2.646550e+04
## floor3 5.832920e+04
## floor3.5 .
For an optimal value of \(\lambda = 326.739\) given by cross_validation un lambda optimal obtenue par la méthode de cross validation, coefficients of sqft_lot, sqft_basement, yr.renovated are closed to zeros, hence we can remove thoses variables from future regression models.
data = data[, -c(5, 11, 13)]
train = data[train_ind,]
test = data[-train_ind,]
Best subset models
# FORWARD STEPWISE SELECTION
regfw.subset = regsubsets(price ~ ., train, nbest = 1, nvmax = ncol(data)-1, method= "forward")
regfwd.summary = summary(regfw.subset)
plot(regfw.subset, scale = "adjr2")
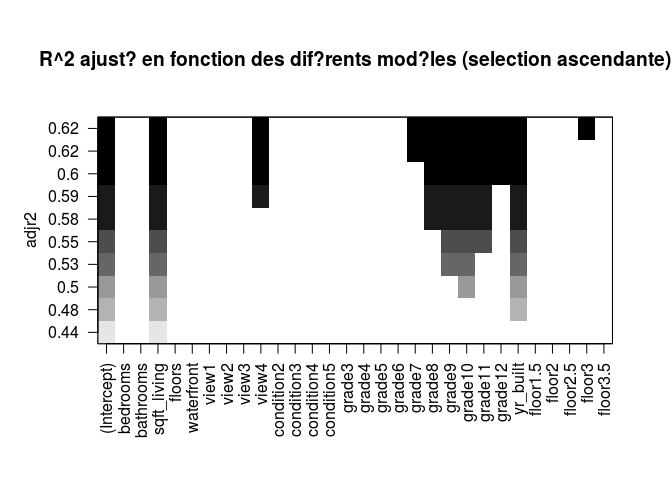
# BACKWARD STEPWISE SELECTION
regfw.subset = regsubsets(price ~ ., train, nbest = 1, nvmax = ncol(data)-1, method= "backward")
regfwd.summary = summary(regfw.subset)
plot(regfw.subset, scale = "adjr2", main = "R^2 ajusté en fonction des diférents modéles (selection descendante)")
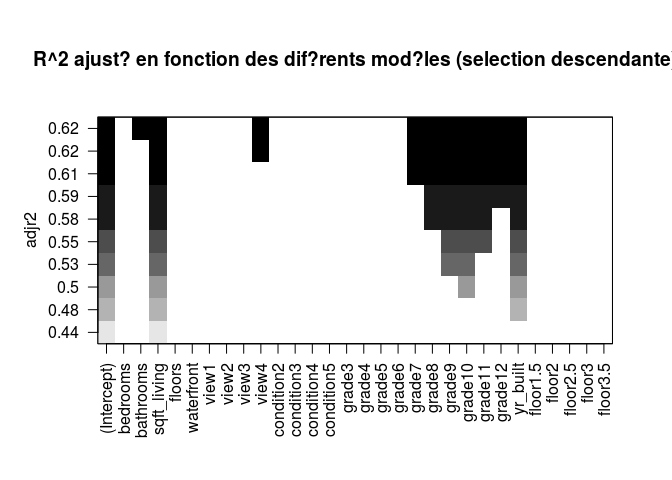
Selection of the best model using cross validation.
# CROSS VALIDATION
folds = sample(rep(1:10, length = nrow(train)))
cv.errors = matrix(NA, 10, ncol(data) - 1)
prediction.regsubsets = function(object, newdata, id, ...){
form = as.formula(object$call[[2]]) #extract object model formula for y ~ x
mat = model.matrix(form, newdata) #set prediction matrix
coefi = coef(object, id = id) #obtain matrix of coefficients
mat[, names(coefi)] %*% coefi #calculate predictions matrix
}
for(k in 1:10){
best.fit = regsubsets(price ~ . , data = train[folds != k, ], nvmax = ncol(data)-1,
method = "forward")
for(i in 1:(ncol(data)-1)){
pred = prediction.regsubsets(best.fit, train[folds == k, ], id = i)
cv.errors[k, i] = mean((train$price[folds == k] - pred) ^ 2)
}
}
# Reordering variables and trying again:
rmse.cv = sqrt(apply(cv.errors, 2, mean))
plot(rmse.cv, pch = ncol(data)-1, type = "b",xlab = "Nombre de variable explicatives pour les différents meilleures modéles")
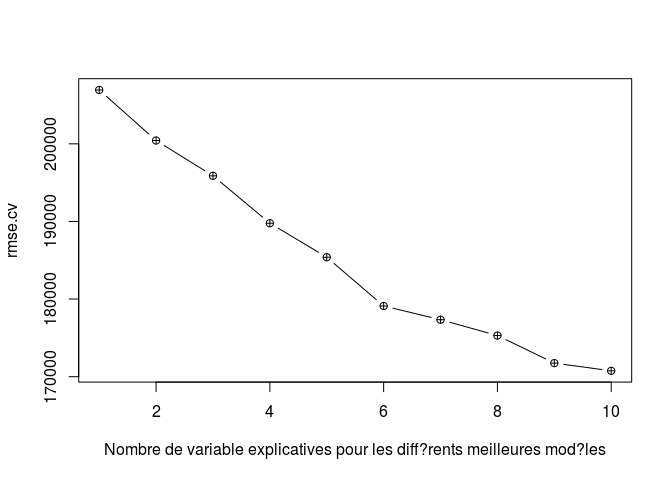
# Best model over the training set
which.min(rmse.cv)
## [1] 10
The best-validated model is, therefore, the model 10, it will be used on our test data.
x.test = model.matrix(price ~., data = test)
# Calculer le MSE pour tous les modéles (et voir si le modéle choisi minimise le MSE des données de test)
coefi = coef(regfw.subset, id = 10)
pred = x.test[ , names(coefi)] %*% coefi
paste("Modele 10, RMSE = ",sqrt(mean((test$price - pred) ^ 2)))
## [1] "Modele 10, RMSE = 171457.71092754"
Compared to the simple regression model, an explanatory variable, the RMSE test has decreased by 30,000. This is partly explained by the fact that the last model is more flexible.
PCA
The approach of the main components is another statisticals technique to find the variables Xi of the model which explains the maximum variance of the dependent variable.
pcr.fit = pcr(price ~., data=data, scale=T, validation="CV", ncomp=27)
summary(pcr.fit)
## Data: X dimension: 19583 29
## Y dimension: 19583 1
## Fit method: svdpc
## Number of components considered: 27
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 276527 243636 205658 201720 201623 197521 196540
## adjCV 276527 243635 205645 201699 201606 197500 196523
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 195857 192119 191811 191778 191749 191070 190893
## adjCV 195858 191866 191772 191784 191790 191020 190961
## 14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
## CV 190672 190386 190048 189708 189251 188639
## adjCV 190682 190315 189983 189860 189237 188629
## 20 comps 21 comps 22 comps 23 comps 24 comps 25 comps
## CV 188502 188433 178661 178591 167097 166197
## adjCV 188483 188414 178635 178578 167075 166177
## 26 comps 27 comps
## CV 166213 166228
## adjCV 166193 166206
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## X 15.22 22.23 27.71 32.84 37.47 41.81 45.81
## price 22.39 44.72 46.83 46.91 49.05 49.56 49.91
## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
## X 49.67 53.47 57.11 60.69 64.23 67.73 71.20
## price 51.97 51.97 51.97 51.99 52.44 52.44 52.56
## 15 comps 16 comps 17 comps 18 comps 19 comps 20 comps
## X 74.64 78.05 81.45 84.83 88.03 91.07
## price 52.77 52.95 52.96 53.31 53.64 53.73
## 21 comps 22 comps 23 comps 24 comps 25 comps 26 comps
## X 93.73 95.61 97.13 98.40 99.41 99.99
## price 53.77 58.42 58.45 63.64 64.03 64.04
## 27 comps
## X 100.00
## price 64.04
validationplot(pcr.fit, val.type = "RMSEP")
 The optimal value M of the number of explanatory variables is 27. However, we note that from 24 variables, the RMSE, as well as variance of the model are close to the optimal value. As a result, M = 24 will be used to measure our MSE on the test set.
The optimal value M of the number of explanatory variables is 27. However, we note that from 24 variables, the RMSE, as well as variance of the model are close to the optimal value. As a result, M = 24 will be used to measure our MSE on the test set.
pcr.fit = pcr(price ~ ., data=train, scale=T, validation="CV", ncomp= 24)
pcr.pred = predict(pcr.fit, test, ncomp = 24)
sqrt(mean((pcr.pred - test$price) ^2))
## [1] 167071.6
Regression tree
The last technique used will be regression trees. Let’s start with a single regression tree.
tree.fit = tree(price~., data=train)
summary(tree.fit)
##
## Regression tree:
## tree(formula = price ~ ., data = train)
## Variables actually used in tree construction:
## [1] "grade" "sqft_living" "yr_built"
## Number of terminal nodes: 8
## Residual mean deviance: 3.515e+10 = 4.815e+14 / 13700
## Distribution of residuals:
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -758400 -122300 -28350 0 93680 1358000
plot(tree.fit)
text(tree.fit, pretty=0)
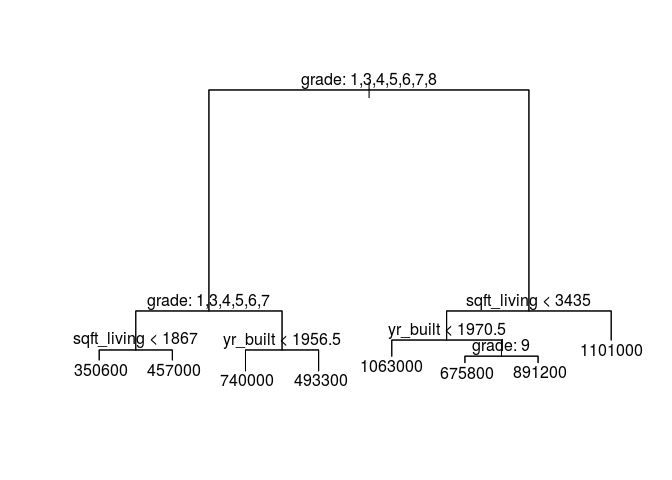
tree.pred = predict(tree.fit, test)
sqrt(mean((test$price - tree.pred)^2))
## [1] 191385.4
With the method of cross validation, it is possible to determine an optimal tree size. R provides a function for this cv.tree.
plot(tree.cvsize, tree, cvdev, type="b")
tree.min = which.min(tree.cv$size)
tree.min
The optimal depth obtained above corresponds to the initial depth of our tree. The RMSE is high, compared to the scores of the other methods; doubly because using a single tree to predict the price is highly variant.
Random Forest improves a lot the uses of regression trees, recovering the result of several regression trees, constructed differently, independently, using bootstrapped data. It has the effect of reducing a lot the variance of the initial method. Each split in each tree is computed from some attributes m < number of total preachers. Here are the results for m = 5.
rf.fit = randomForest(price~., data=train, mtry=5, ntree=50, importance=TRUE)
rf.pred = predict(rf.fit, test)
sqrt(mean((test$price - rf.pred)^2))
## [1] 163452.1
The RMSE is much better than for a single tree, which seems logical. This method gets the best score on the RMSE test.
Neural networks
Finally, I wanted to try neural network and see if it will beat the current best RMSE test. I didn’t. Even worse, it fails entirely. I was not able to conclude the reason for this failure because neural networks are always tricky to debug, even though they are sometimes very powerful.
Moreover, in our cases, attributes are already engineered. Hence we can use simpler model other than neural network, which is very powerful to do the feature processing at every layer, for us.
At the end of 100 eras (passage on the data) is ~180000.
Conclusion
Resume
After cleaning our initial data set, by removing unuseful attributes, decorrelating those remaining, and removing Outliers, we were able to train several models. Each model predicted the price of the house according to a dozen of attributes maximum. The simple linear regression of the price as a function of the surface allowed us to establish a baseline minimum error score of RMSE test: 208662.5). Then, we used more complex models.
- Lasso regression (RMSE test: 164778.5)
- The approach of the best subsets (RMSE test: 171457.7),
- The principal components approach (RMSE test: 167071.6),
- 1 tree of regression (RMSE test: 191385.4)
- Random forest (RMSE test: 162527.1).
Analyse
This percentage of error is high, but the exact price of a house at the scale of a large geographic area is quite complicated, and some features were not taken into account (such as leasing). Moreover, the models used assumed a linear relationship between the predicates, and the output variable, which is not necessarily the case, given the best performance obtained by the random forest technique.
Kaggle comparison on RMSE test
By comparing, results obtained with those from the best ranked script, It appears that I get better prediction than their model. The difference might comes from better preprocessing.